前言
这个专题我们用来探讨回溯算法,回溯算法是一种递归算法,它在一棵树上的深度优先遍历(因为要遍历整棵树,所以时间复杂度一般都不低)。
回溯算法和 dfs 算法不同的点在于,回溯算法在遍历的过程中,会对每一个节点进行判断,如果不符合条件,就会回溯到上一个节点,然后再进行遍历。我们举一个最简单的例子来区别什么时候使用回溯算法,什么时候使用 dfs 算法。
比如我们有一个数组,数组中的每一个元素都是一个选择,我们要从这些选择中,选择一个符合条件的元素。那么我们就可以使用回溯算法,因为我们在遍历的过程中,可以对每一个元素进行判断,如果不符合条件,就回溯到上一个元素,然后再进行遍历。
但是如果我们要从这些选择中,选择出所有符合条件的元素,那么我们就需要使用 dfs 算法,因为我们需要遍历整棵树,然后把所有符合条件的元素都找出来。
回溯算法的思想非常简单,大致上可以分为以下几个步骤:
- 路径:做出一个选择
- 选择:从选择列表中做出一个选择
- 条件:符合结束条件,就把这个选择加入到结果中
- 撤销:撤销选择
伪代码如下:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做出选择
backtrack(路径, 选择列表)
撤销选择基础题
17. Letter Combinations of a Phone Number
这道题的描述是给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
test cases:
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
Input: digits = ""
Output: []这道题的思路就是回溯算法的思路,我们可以把每一个数字对应的字母都放到一个数组中,然后对这个数组进行回溯,最后得到所有的结果。具体来说,每一个电话号码都可以看成是一个树,比如 2 可以看成是这样的一棵树,对应的分支就是 2 对应的字母。那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
# 用一个字典来存储每一个数字对应的字母
dic = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz"
}
res = []
def backtrack(index, path):
if index == len(digits): # 如果索引和数字的长度相等,说明已经遍历完了
res.append("".join(path))
return
possible = dic[digits[index]]
for letter in possible:
path.append(letter) # 做出选择
backtrack(index + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [])
return res复杂度分析:
- 时间复杂度:O(3^m 4^n),其中 m 是输入中对应 3 个字母的数字个数(包括数字 2、3、4、5、6、8),n 是输入中对应 4 个字母的数字个数(包括数字 7、9),m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时,不同的字母组合一共有 3^m 4^n 种,需要遍历每一种字母组合。
- 空间复杂度:O(m+n),其中 m 是输入中对应 3 个字母的数字个数,n 是输入中对应 4 个字母的数字个数,m+n 是输入数字的总个数。除了返回值以外,空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数,哈希表的大小与输入无关,可以看成常数,递归调用层数最大为 m+n。
39. Combination Sum
这道题的描述是给定一个无重复元素的数组 candidates 和一个目标数 target,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
test cases:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 candidates = [2,3,6,7],target = 7 的时候,我们可以看成是这样的一棵树:
2
/ | \
2 3 6
/ \ / \ / \
2 3 2 3 2 3那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
def backtrack(index, path, rest):
if rest == 0: # 如果目标数为 0,说明已经遍历完了
res.append(path[:])
return
if rest < 0: # 如果目标数小于 0,说明不是正确的结果
return
for i in range(index, len(candidates)):
path.append(candidates[i]) # 做出选择
backtrack(i, path, rest - candidates[i]) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [], target)
return res复杂度分析:
- 时间复杂度:O(S),其中 S 是所有可行解的长度之和。在最坏的情况下,所有的组合都是可行的,例如 candidates = [1,1,1,1,1,1,1,1,1,1,1],target = 11。在这种情况下,一共有 O(2^N) 个组合,每一个组合的长度都是 O(N),因此时间复杂度为 O(N * 2^N)。在最好的情况下,组合里的数字都是 1,此时时间复杂度为 O(N)。
- 空间复杂度:O(target)。除了答案数组之外,空间复杂度取决于递归的栈深度,在最坏的情况下,需要递归 O(target) 层。
40. Combination Sum II
这道题的描述是给定一个数组 candidates 和一个目标数 target,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
test cases:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output: [[1,1,6],[1,2,5],[1,7],[2,6]]
Input: candidates = [2,5,2,1,2], target = 5
Output: [[1,2,2],[5]]这道题和上一道题的区别在于,上一道题中的数组中的数字可以无限制重复被选取,而这道题中的数组中的数字在每个组合中只能使用一次。那么我们就可以对这道题进行一些修改,比如在递归的时候,我们可以把索引加一,这样就可以保证每个数字只会被使用一次。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
def backtrack(start, path, rest):
if rest == 0: # 如果目标数为 0,说明已经遍历完了
res.append(path[:])
return
if rest < 0: # 如果目标数小于 0,说明不是正确的结果
return
for i in range(start, len(candidates)):
if i > start and candidates[i] == candidates[i - 1]:
# 如果当前的数和前一个数相等,说明已经遍历过了,直接返回
# 举个例子,比如 candidates = [1,1,2,5,6,7,10],target = 8
# 当 i = 1 的时候,path = [1],rest = 7,此时 i > start 并且 candidates[i] == candidates[i - 1]
# 所以直接跳过,不进行递归
continue
path.append(candidates[i]) # 做出选择
backtrack(i + 1, path, rest - candidates[i]) # 进入下一层决策树
path.pop() # 撤销选择
candidates.sort() # 先对数组进行排序
backtrack(0, [], target)
return res复杂度分析:
- 时间复杂度:O(S),其中 S 是所有可行解的长度之和。在最坏的情况下,所有的组合都是可行的,例如 candidates = [1,1,1,1,1,1,1,1,1,1,1],target = 11。在这种情况下,一共有 O(2^N) 个组合,每一个组合的长度都是 O(N),因此时间复杂度为 O(N * 2^N)。在最好的情况下,组合里的数字都是 1,此时时间复杂度为 O(N)。
- 空间复杂度:O(target)。除了答案数组之外,空间复杂度取决于递归的栈深度,在最坏的情况下,需要递归 O(target) 层。
216. Combination Sum III
这道题的描述是给定一个整数 k 和一个整数 n,找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
test cases:
Input: k = 3, n = 7
Output: [[1,2,4]]
Input: k = 3, n = 9
Output: [[1,2,6],[1,3,5],[2,3,4]]
Input: k = 4, n = 1
Output: []
Input: k = 3, n = 2
Output: []
Input: k = 9, n = 45
Output: [[1,2,3,4,5,6,7,8,9]]这道题和上一道题的区别在于,上一道题中的数组中的数字可以无限制重复被选取,而这道题中的数组中的数字在每个组合中只能使用一次。那么我们就可以对这道题进行一些修改,比如在递归的时候,我们可以把索引加一,这样就可以保证每个数字只会被使用一次。
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res = []
def backtrack(start, path, rest):
if rest == 0 and len(path) == k: # 如果目标数为 0,且路径的长度和 k 相等,说明已经遍历完了
res.append(path[:])
return
if rest < 0 or len(path) >= k: # 如果目标数小于 0,或者路径的长度大于 k,说明不是正确的结果
return
for i in range(start, 10):
path.append(i) # 做出选择
backtrack(i + 1, path, rest - i) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(1, [], n)
return res复杂度分析:
- 时间复杂度:O(9!),其中 9! = 362880。
- 空间复杂度:O(k),其中 k 为组合的长度。
46. Permutations
这道题的描述是给定一个不含重复数字的数组 nums,返回这些数字的所有可能的全排列。你可以按任意顺序返回答案。
test cases:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Input: nums = [0,1]
Output: [[0,1],[1,0]]
Input: nums = [1]
Output: [[1]]这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 nums = [1,2,3] 的时候,我们可以看成是这样的一棵树:
1
/ | \
2 3 2
/ \ / \ / \
3 2 2 1 1 3那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
def backtrack(path):
if len(path) == len(nums): # 如果路径的长度和数组的长度相等,说明已经遍历完了
res.append(path[:])
return
for num in nums:
if num in path: # 如果当前的数字已经在路径中了,说明已经遍历过了,直接返回
continue
path.append(num) # 做出选择
backtrack(path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack([])
return res实际上这道题也可以使用 python 的包来解决,比如 itertools 中的 permutations 函数,这个函数可以返回一个数组的所有的组合,比如:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(itertools.permutations(nums))复杂度分析:
- 时间复杂度:O(N * N!),其中 N 为数组的长度。
- 空间复杂度:O(N * N!),其中 N 为数组的长度。
47. Permutations II
test cases:
Input: nums = [1,1,2]
Output: [[1,1,2],[1,2,1],[2,1,1]]
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]这道题和上一道题的区别在于,这道题中的数组中的数字可以重复出现。那么我们就可以使用 counter 来记录每个数字出现的次数,然后在回溯的前后,加减相应的次数即可。
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
results = []
def backtrack(path, counter):
if len(path) == len(nums):
# 当路径的长度和数组的长度相等的时候,说明已经遍历完了
results.append(path[:])
return
for num in counter:
if counter[num] > 0: # 如果当前数字的次数大于 0,说明可以使用
path.append(num)
counter[num] -= 1 # 次数减一
backtrack(path, counter)
path.pop() # 撤销选择
counter[num] += 1 # 次数加一
backtrack([], Counter(nums))
return results或者我们可以使用 visited 数组来记录每个数字是否被访问过,这样就不需要使用 counter 了。
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
def backtrack(res, cur, nums, visited):
if len(cur) == len(nums):
res.append(cur[:])
for i in range(len(nums)):
if (visited[i] == 1) or (i > 0 and nums[i] == nums[i - 1] and visited[i - 1] == 0):
continue
visited[i] = 1
cur.append(nums[i])
backtrack(res, cur, nums, visited)
visited[i] = 0
cur.pop()
return res
res = []
boolean = [0 for _ in range(len(nums))]
nums.sort()
return backtrack(res, [], nums, boolean)实际上这道题也可以使用 python 的包来解决,比如 itertools 中的 permutations 函数,这个函数可以返回一个数组的所有的组合,比如:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(set(itertools.permutations(nums)))复杂度分析:
- 时间复杂度:O(N * N!),其中 N 为数组的长度。
- 空间复杂度:O(N * N!),其中 N 为数组的长度。
78. Subsets
test cases:
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
Input: nums = [0]
Output: [[],[0]]这道题的描述是给定一个不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。解集不能包含重复的子集。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 nums = [1,2,3] 的时候,我们可以看子集树是这样的一棵树:
[]
/ | \
1 2 3
/ \ / \ / \
2 3 3 1 1 2
/ \ / \ / \ / \ / \ / \
3 1 1 2 2 1 3 3 2 2 1实际上这是错的,因为这棵树中有重复的子集,比如 [1,2] 和 [2,1],所以我们需要对这棵树进行剪枝,剪枝的方法就是在递归的时候,传入一个 start 的参数,这个参数表示当前数字的下标,比如我们在遍历到 2 的时候,start 就是 1,那么我们就只需要遍历 2 之后的数字,这样就不会出现重复的子集了。
那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
def backtrack(start, path):
res.append(path[:])
for i in range(start, len(nums)):
path.append(nums[i]) # 做出选择
backtrack(i + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [])
return res实际上这道题也可以使用 python 的包来解决,比如 itertools 中的 combinations 函数,这个函数可以返回一个数组的所有的组合,比如:
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
return chain.from_iterable(chain([combinations(nums, i) for i in range(len(nums) + 1)]))复杂度分析:
- 时间复杂度:O(N * 2^N),其中 N 为数组的长度。
- 空间复杂度:O(N * 2^N),其中 N 为数组的长度。
90. Subsets II
test cases:
Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]
Input: nums = [0]
Output: [[],[0]]这道题和上一道题的区别在于,这道题的数组中包含重复的元素,所以我们需要对这棵树进行剪枝,剪枝的方法就是在递归的时候,传入一个 start 的参数,这个参数表示当前数字的下标,比如我们在遍历到 2 的时候,start 就是 1,那么我们就只需要遍历 2 之后的数字,这样就不会出现重复的子集了。而且要注意的是,我们在遍历的时候,如果当前的数字和前一个数字相等,说明已经遍历过了,直接返回。
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
def backtrack(start, path):
res.append(path[:])
for i in range(start, len(nums)):
if i > start and nums[i] == nums[i - 1]: # 如果当前的数字和前一个数字相等,说明已经遍历过了,直接返回
continue
path.append(nums[i]) # 做出选择
backtrack(i + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
nums.sort() # 先对数组进行排序
backtrack(0, [])
return res实际上这道题也可以使用 python 的包来解决,比如 itertools 中的 combinations 函数,这个函数可以返回一个数组的所有的组合,比如:
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
return set([tuple(sorted(item)) for item in chain.from_iterable(chain([combinations(nums, i) for i in range(len(nums) + 1)]))])复杂度分析:
- 时间复杂度:O(N * 2^N),其中 N 为数组的长度。
- 空间复杂度:O(N * 2^N),其中 N 为数组的长度。
进阶题
22. Generate Parentheses
test cases:
Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]
Input: n = 1
Output: ["()"]这道题的描述是给定一个整数 n,生成所有由 n 对括号组成的有效组合。有效的组合需要满足:左括号必须以正确的顺序闭合。
这道题的思路也是回溯算法的思路,我们可以把每一个括号都看成是一个树,比如 n=3 的时候,我们可以看成是这样的一棵树:
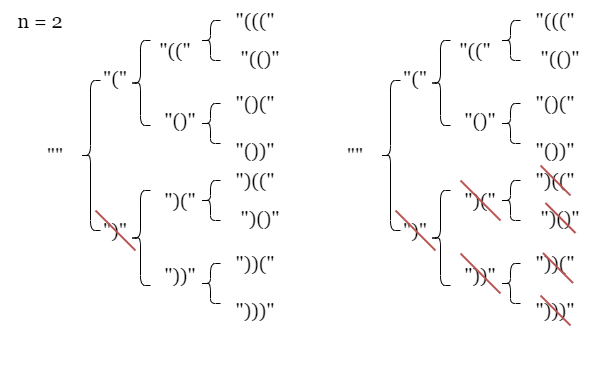
那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
def backtrack(left, right, path):
if left == 0 and right == 0: # 如果左右括号都用完了,说明已经遍历完了
res.append("".join(path))
return
if left > right: # 如果左括号的数量大于右括号的数量,说明不符合条件,直接返回
return
if left > 0: # 如果左括号的数量大于 0,可以加一个左括号
path.append("(")
backtrack(left - 1, right, path)
path.pop()
if right > 0: # 如果右括号的数量大于 0,可以加一个右括号
path.append(")")
backtrack(left, right - 1, path)
path.pop()
backtrack(n, n, [])
return res复杂度分析:
- 时间复杂度:O(4^n / sqrt(n)),在回溯过程中,每个答案需要 O(n) 的时间复制到答案数组中。
- 空间复杂度:O(n),除了答案数组之外,我们所需要的空间取决于递归栈的深度,每一层递归函数需要 O(1) 的空间,最多递归 2n 层,因此空间复杂度为 O(n)。
79. Word Search
test cases:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false这道题的描述是给定一个二维网格和一个单词,找出该单词是否存在于网格中。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
这道题的思路也是回溯算法的思路,我们可以把每一个字母都看成是一个树,比如 board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]],word = "ABCCED" 的时候,我们可以看成是这样的一棵树:
A
/ | \
B S D
/ \ / \ / \
C D F E E C
/ \ / \ / \ / \ / \ / \
C E C C C S E E C C那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
def backtrack(i, j, index):
if index == len(word): # 如果索引和单词的长度相等,说明已经遍历完了
return True
if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]) or board[i][j] != word[index]: # 如果索引越界或者当前的字母和单词中的字母不相等,说明不符合条件,直接返回
return False
board[i][j] = "#" # 做出选择
res = backtrack(i + 1, j, index + 1) or backtrack(i - 1, j, index + 1) or backtrack(i, j + 1, index + 1) or backtrack(i, j - 1, index + 1) # 进入下一层决策树
board[i][j] = word[index] # 撤销选择
return res
for i in range(len(board)):
for j in range(len(board[0])):
if backtrack(i, j, 0):
return True
return False复杂度分析:
- 时间复杂度:O(M * N * 4^L),其中 M 和 N 分别为二维网格的高和宽,L 为字符串 word 的长度。在每次调用函数 backtrack 时,除了第一次可以进入 4 个分支以外,其余时间我们最多会进入 3 个分支(因为每个位置只能使用一次,所以走过来的分支没法走回去)。由于单词长为 L,故 backtracking 函数的时间复杂度为 O(3^L)。而我们要执行 O(M * N) 次检查,故总时间复杂度为 O(M * N * 3^L)。
- 空间复杂度:O(L),其中 L 为字符串 word 的长度。主要为递归调用的栈空间。
93. Restore IP Addresses
test cases:
Input: s = "25525511135"
Output: ["255.255.11.135","255.255.111.35"]
Input: s = "0000"
Output: ["0.0.0.0"]
Input: s = "101023"
Output: ["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]这道题的描述是给定一个只包含数字的字符串 s,返回所有可能从 s 获得的有效 IP 地址。你可以按任何顺序返回答案。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 s = "25525511135" 的时候,我们可以看成是这样的一棵树:
2
/ | \
5 5 5
/ \ / \ / \
5 5 5 5 5 5
/ \ / \ / \ / \ / \ / \
2 5 2 5 2 5 2 5 2 5那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
res = []
def backtrack(start, path):
if start == len(s) and len(path) == 4: # 如果索引和字符串的长度相等,说明已经遍历完了
res.append(".".join(path))
return
if len(path) > 4: # 如果路径的长度大于 4,说明不符合条件,直接返回
return
for i in range(start, len(s)):
if s[start] == "0" and i > start: # 如果当前的数字是 0,且索引不相等,说明是连续的 0,不符合条件,直接返回
return
num = int(s[start:i + 1])
if num > 255: # 如果当前的数字大于 255,说明不符合条件,直接返回
return
path.append(str(num)) # 做出选择
backtrack(i + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [])
return res复杂度分析:
- 时间复杂度:O(1),因为 IP 地址的长度是固定的。
- 空间复杂度:O(1),因为 IP 地址的长度是固定的。
131. Palindrome Partitioning
test cases:
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
Input: s = "a"
Output: [["a"]]这道题的描述是给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。
这道题的思路也是回溯算法的思路,我们可以把每一个字母都看成是一个树,比如 s = "aab" 的时候,我们可以看成是这样的一棵树:
a
/ | \
a a b
/ \ / \ / \
a b a b a b
/ \ / \ / \ / \ / \ / \
b a b a b a b a b a那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
def backtrack(index, path):
if index == len(s): # 如果索引和字符串的长度相等,说明已经遍历完了
res.append(path[:])
return
for i in range(index, len(s)):
if self.isPalindrome(s[index:i + 1]): # 如果当前的字符串是回文串,就可以继续遍历
path.append(s[index:i + 1]) # 做出选择
backtrack(i + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [])
return res
def isPalindrome(self, s: str) -> bool:
return s == s[::-1]复杂度分析:
- 时间复杂度:O(N * 2^N),其中 N 为字符串的长度。
- 空间复杂度:O(N * 2^N),其中 N 为字符串的长度。
254. Factor Combinations
test cases:
Input: n = 1
Output: []
Input: n = 37
Output: []
Input: n = 12
Output: [[2,6],[2,2,3],[3,4]]
Input: n = 32
Output: [[2,16],[2,2,8],[2,2,2,4],[2,2,2,2,2],[2,4,4],[4,8]]这道题的描述是给定一个整数 n,返回 n 的因数所有可能的组合。因数是一个数能被另一个数整除的数。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 n = 12 的时候,我们可以看成是这样的一棵树:
12
/ | \
2 3 4
/ \ / \ / \
2 6 3 4 4 3
/ \ / \ / \ / \ / \ / \
3 4 2 3 2 2 3 2 2 2那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def getFactors(self, n: int) -> List[List[int]]:
res = []
def backtrack(index, path, target):
if target == 1 and len(path) > 1: # 如果目标数为 1,且路径的长度大于 1,说明已经遍历完了
res.append(path[:])
return
for i in range(index, target + 1):
if target % i == 0: # 如果当前的数能被目标数整除,就可以继续遍历
path.append(i) # 做出选择
backtrack(i, path, target // i) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(2, [], n)
return res复杂度分析:
- 时间复杂度:O(N * logN),其中 N 为整数 n 的大小。
- 空间复杂度:O(N * logN),其中 N 为整数 n 的大小。
401. Binary Watch
test cases:
Input: turnedOn = 1
Output: ["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"]
Input: turnedOn = 9
Output: []这道题的描述是给定一个非负整数 turnedOn,表示当前亮着的 LED 的数量,返回所有可能的时间。你可以按任意顺序返回答案。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 turnedOn = 1 的时候,我们可以看成是这样的一棵树:
0
/ | \
1 2 4
/ \ / \ / \
2 4 3 5 5 6
/ \ / \ / \ / \ / \ / \
3 5 4 6 5 7 6 8 7 9那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def readBinaryWatch(self, turnedOn: int) -> List[str]:
res = []
def backtrack(index, path, hour, minute):
if hour > 11 or minute > 59: # 如果小时大于 11 或者分钟大于 59,说明不符合条件,直接返回
return
if turnedOn == 0: # 如果亮着的 LED 的数量为 0,说明已经遍历完了
res.append(str(hour) + ":" + "0" * (minute < 10) + str(minute))
return
for i in range(index, 10):
if i < 4: # 如果当前的索引小于 4,说明是小时
backtrack(i + 1, path, hour + (1 << i), minute) # 进入下一层决策树
else: # 如果当前的索引大于等于 4,说明是分钟
backtrack(i + 1, path, hour, minute + (1 << (i - 4))) # 进入下一层决策树
backtrack(0, [], 0, 0)
return res复杂度分析:
- 时间复杂度:O(1)。
- 空间复杂度:O(1)。
526. Beautiful Arrangement
test cases:
Input: n = 2
Output: 2
Input: n = 1
Output: 1这道题的描述是给定一个正整数 n,返回所有可能的 n 个数的美丽排列。如果一个数组的第 i 位元素能被 i 整除,那么就认为这个数组是一个美丽的排列。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 n = 2 的时候,我们可以看成是这样的一棵树:
1
/ | \
2 1 2那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def countArrangement(self, n: int) -> int:
res = []
def backtrack(index, path):
if index == n + 1: # 如果索引和 n + 1 相等,说明已经遍历完了
res.append(path[:])
return
for i in range(1, n + 1):
if i in path: # 如果当前的数字已经在路径中了,说明已经遍历过了,直接返回
continue
if i % index == 0 or index % i == 0: # 如果当前的数字能被索引整除,或者索引能被当前的数字整除,就可以继续遍历
path.append(i) # 做出选择
backtrack(index + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(1, [])
return len(res)复杂度分析:
- 时间复杂度:O(k),其中 k 为符合条件的排列的个数。
- 空间复杂度:O(n),其中 n 为正整数 n 的大小。
784. Letter Case Permutation
test cases:
Input: s = "a1b2"
Output: ["a1b2","a1B2","A1b2","A1B2"]
Input: s = "3z4"
Output: ["3z4","3Z4"]这道题的描述是给定一个字符串 s,返回所有可能的大小写字母全排列。字母区分大小写。
这道题的思路也是回溯算法的思路,我们可以把每一个字母都看成是一个树,比如 s = "a1b2" 的时候,我们可以看成是这样的一棵树:
a
/ | \
a A a
/ \ / \ / \
a b A b a b
/ \ / \ / \ / \ / \ / \
b 2 B 2 b 2 B 2 b 2那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def letterCasePermutation(self, s: str) -> List[str]:
res = []
def backtrack(index, path):
if index == len(s): # 如果索引和字符串的长度相等,说明已经遍历完了
res.append("".join(path))
return
if s[index].isdigit(): # 如果当前的字符是数字,就可以继续遍历
path.append(s[index]) # 做出选择
backtrack(index + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
else: # 如果当前的字符是字母,就可以继续遍历
path.append(s[index].lower()) # 做出选择
backtrack(index + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
path.append(s[index].upper()) # 做出选择
backtrack(index + 1, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [])
return res复杂度分析:
- 时间复杂度:O(N * 2^N),其中 N 为字符串的长度。
- 空间复杂度:O(N * 2^N),其中 N 为字符串的长度。
797. All Paths From Source to Target
test cases:
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Input: graph = [[1],[]]
Output: [[0,1]]
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]这道题的描述是给定一个有 n 个结点的有向无环图,找到所有从 0 到 n - 1 的路径并输出(不要求按顺序)。
这道题的思路也是回溯算法的思路,我们可以把每一个结点都看成是一个树,比如 graph = [[1,2],[3],[3],[]] 的时候,我们可以看成是这样的一棵树:
0
/ | \
1 3 3
/ \ / \ / \
2 3 3 3 3 3
/ \ / \ / \ / \ / \ / \
3 3 3 3 3 3 3 3 3 3那么我们就可以对这棵树进行回溯,得到所有的结果。
class Solution:
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
res = []
def backtrack(index, path):
if index == len(graph) - 1: # 如果索引和图的长度相等,说明已经遍历完了
res.append(path[:])
return
for i in graph[index]:
path.append(i) # 做出选择
backtrack(i, path) # 进入下一层决策树
path.pop() # 撤销选择
backtrack(0, [0])
return res复杂度分析:
- 时间复杂度:O(N * 2^N),其中 N 为图的长度。
- 空间复杂度:O(N * 2^N),其中 N 为图的长度。
842. Split Array into Fibonacci Sequence
test cases:
Input: "123456579"
Output: [123,456,579]
Input: "11235813"
Output: [1,1,2,3,5,8,13]
Input: "112358130"
Output: []
Input: "0123"
Output: []
Input: "1101111"
Output: [110, 1, 111]这道题的描述是给定一个数字字符串 S,比如 S = "123456579",我们可以把它分成多个斐波那契式的序列,比如 [123, 456, 579]。斐波那契式序列是一个序列,其中每个数字都是前面两个数字的和。形式上,给定一个斐波那契式序列,我们要从其中删除最少一个数字,使得剩余的数字构成一个严格递增的序列。返回所有可能的情况。
这道题的思路也是回溯算法的思路,我们可以把每一个数字都看成是一个树,比如 S = "123456579" 的时候,我们可以看成是这样的一棵树:
1
/ | \
2 2 2
/ \ / \ / \
3 3 3 3 3 3
/ \ / \ / \ / \ / \ / \
4 4 4 4 4 4 4 4 4 4那么我们就可以对这棵树进行回溯,得到所有的结果。
未完待续126. Word Ladder II
test cases:
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output:
[
["hit","hot","dot","dog","cog"],
["hit","hot","lot","log","cog"]
]
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: []这道题的描述是给定两个单词(beginWord 和 endWord)和一个字典 wordList,找到从 beginWord 到 endWord 的所有最短转换序列。转换需遵循如下规则:
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典中的单词。
我们当然可以使用 bfs 来做,每一个东西都存储在 queue 当中,但是这样会 mle:
class Solution:
def findLadders(self, beginWord: str, endWord: str, wordList):
if not endWord or not beginWord or not wordList or endWord not in wordList or beginWord == endWord:
return []
graph = collections.defaultdict(list)
for word in wordList:
for i in range(len(beginWord)):
graph[word[:i] + "*" + word[i+1:]].append(word)
print(graph)
ans = []
q = collections.deque([(beginWord, [beginWord])])
visited = set()
visited.add(beginWord)
while q and not ans:
length = len(q)
localvisited = set()
for _ in range(length):
word, path = q.popleft()
for i in range(len(beginWord)):
candidate = word[:i] + "*" + word[i+1:]
for nxt in graph[candidate]:
if nxt == endWord:
ans.append(path + [endWord])
if nxt not in visited:
localvisited.add(nxt)
q.append((nxt, path + [nxt]))
visited = visited.union(localvisited)
return ans
这道题的更好的思路也是回溯算法的思路,我们可以把每一个单词都看成是一个树,比如 beginWord = "hit",endWord = "cog",wordList = ["hot","dot","dog","lot","log","cog"] 的时候,我们可以看成是这样的一棵树:
hit
/ | \
hot dot lot
/ \ / \ / \
dot lot dot lot dot lot
/ \ / \ / \ / \ / \ / \
dog cog dog cog dog cog dog cog那么我们就可以先用 BFS 构建这个 graph,然后对这个 graph 进行回溯,得到所有的结果。
class Solution:
def findLadders(self, beginWord: str, endWord: str, wordList):
wordList.append(beginWord) # needs to add begin word into list for indexing (L126 already consider endword to be in the wordList)
indexes = self.build_indexes(wordList)
distance = self.bfs(endWord, indexes)
results = []
self.dfs(beginWord, endWord, distance, indexes, [beginWord], results)
return results
def build_indexes(self, wordList):
indexes = {}
for word in wordList:
for i in range(len(word)):
key = word[:i] + '%' + word[i + 1:]
if key in indexes:
indexes[key].add(word)
else:
indexes[key] = set([word])
return indexes
def bfs(self, end, indexes): # bfs from end to start
distance = {end: 0}
queue = deque([end])
while queue:
word = queue.popleft()
for next_word in self.get_next_words(word, indexes):
if next_word not in distance:
distance[next_word] = distance[word] + 1
queue.append(next_word)
return distance
def get_next_words(self, word, indexes):
words = set()
for i in range(len(word)):
key = word[:i] + '%' + word[i + 1:]
for w in indexes.get(key, []):
words.add(w)
return words
def dfs(self, curt, target, distance, indexes, path, results):
if curt == target:
results.append(list(path))
return
for word in self.get_next_words(curt, indexes):
if word not in distance: # if there is no a possible way in word ladder
return
if distance[word] != distance[curt] - 1:
continue
path.append(word)
self.dfs(word, target, distance, indexes, path, results)
path.pop()







Comments NOTHING