前言
在二分法中,需要熟练掌握模版,这里提供两个模版,一个是标准模版,另一个是不死模版。
标准模版是大多数 leetcode 模版里提供的答案,而不死模版是来自九章算法的“永不死循环模版”,各有各的好处。
当然,python 也提供 bisect 包,不过在面试中,非常不建议使用,不过对于 OA 解题,很推荐使用这个,因为省时省力。
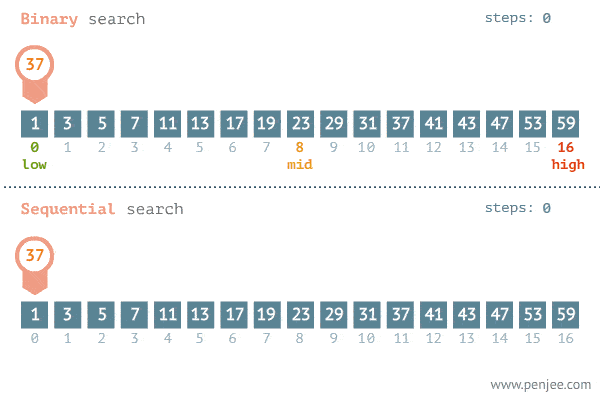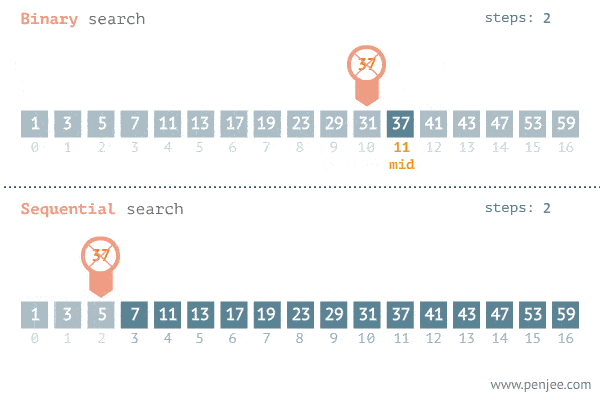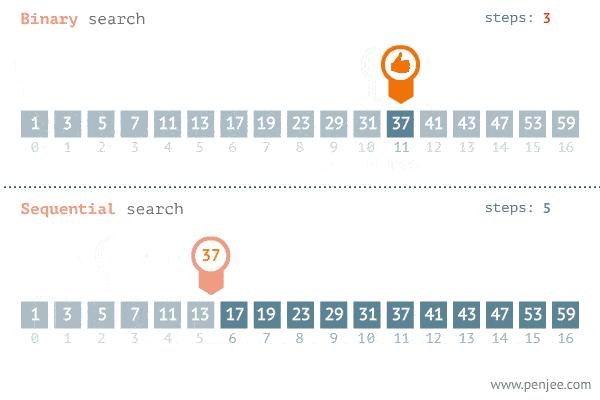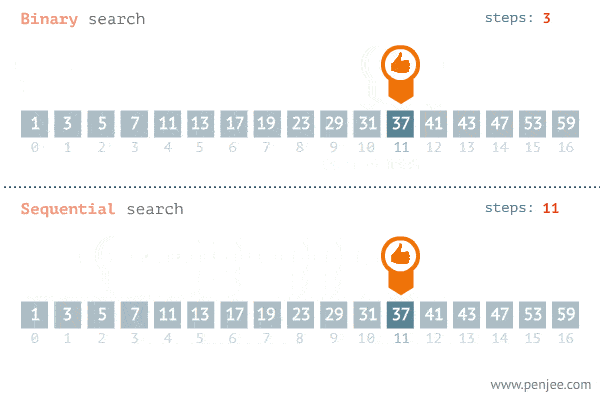
接下来以在一个有序数组中搜寻一个 target 为例题,比较这仨者的区别。
↓ 点击题目就可以直接跳转到 leetcode 题目页面 ↓
基础题
704. Binary Search
test cases:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1标准模版(注意事项已标注在代码中):
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums) - 1
while left <= right: # 这里一定要 <=, left 和 right是允许重合的
mid = left + (right - left) // 2 # 防止累加爆上限
if nums[mid] == target:
return mid
if target < nums[mid]:
right = mid - 1
else:
left = mid + 1
return -1而在不死循环模版里,我们把 while 的条件稍作修改(注意事项已标注在代码中):
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums) - 1
while left + 1 < right: # 这里变成了 +1 <, 相当于在离1个的时候就停止了
mid = left + (right - left) // 2 # 防止累加爆上限
if nums[mid] > target:
right = mid
elif nums[mid] < target:
left = mid
else:
return mid
if nums[left] == target: # 最后对接近的left 做判断
return left
if nums[right] == target: # 最后对接近的right 做判断
return right
return -1直接使用 bisect 包,方便省事,但不推荐面试中使用:
from bisect import bisect_left
def search(self, nums: List[int], target: int) -> int:
num_size = len(nums)
i = bisect_left(nums, target)
return i if i < num_size and nums[i] == target else -1二分法解法的复杂度分析:
Time complexity: O(logN)
Space complexity: O(1)
35. Search Insert Position
这道题与前面那道题不同的一点,就是他要决定插入地点,那么这个就只需要修改一下最后条件即可。
test cases:
Input: nums = [1,3,5,6], target = 5
Output: 2
Input: nums = [1,3,5,6], target = 2
Output: 1
Input: nums = [1,3,5,6], target = 7
Output: 4# 1. 标准模版
def searchInsert(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums) - 1
while left <= right: # 这里一定要 <=, left 和 right是允许重合的
mid = left + (right - left) // 2 # 防止累加爆上限
if nums[mid] == target:
return mid
if target < nums[mid]:
right = mid - 1
else:
left = mid + 1
return left
# 2. 不死模版
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
mid = (left + right) // 2
while left + 1 < right:
mid = (left + right) // 2
print(left, right, mid)
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid
else:
left = mid
if nums[right] < target: # 这里必须先使用right,想想为什么?
return right + 1
if nums[left] < target:
return left + 1
return left
# 3. bisect 包
def searchInsert(self, nums: List[int], target: int) -> int:
return bisect.bisect_left(nums, target)解法的复杂度分析:
Time complexity: O(logN)
Space complexity: O(1)
34. Find First and Last Position of Element in Sorted Array
这道题涉及重复元素,那么要注意,在哪里停下呢?对 if 条件做修改即可
test cases:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
Input: nums = [], target = 0
Output: [-1,-1]# 1. 标准模版
def searchRange(self, nums: List[int], target: int) -> List[int]:
def findLeft(nums, target):
res = -1
start, end = 0, len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] >= target: # 把等于的情况,给到右边,这样就能找到左边界
if nums[mid] == target:
res = mid
end = mid - 1
else:
start = mid + 1
return res
def findRight(nums, target):
res = -1
start, end = 0, len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] <= target: # 把等于的情况,给到左边,这样就能找到右边界
if nums[mid] == target:
res = mid
start = mid + 1
else:
end = mid - 1
return res
if nums == None or len(nums) == 0:
return [-1, -1]
return [findLeft(nums, target), findRight(nums,target)]
# 2. 不死模版
def searchRange(self, nums: List[int], target: int) -> List[int]:
def findLeft(nums, target):
start, end = 0, len(nums) - 1
while start + 1 < end:
mid = start + (end - start) // 2
if nums[mid] >= target: # 把等于的情况,给到右边,这样就能找到左边界
end = mid
else:
start = mid
if nums[start] == target:
return start
if nums[end] == target:
return end
return -1
def findRight(nums, target):
start, end = 0, len(nums) - 1
while start + 1 < end:
mid = start + (end - start) // 2
if nums[mid] > target:
end = mid
else: # 把等于的情况,给到左边,这样就能找到右边界
start = mid
if nums[end] == target: # 这种情况之下为什么要先判断end呢?
return end
if nums[start] == target:
return start
return -1
if nums == None or len(nums) == 0:
return [-1, -1]
return [findLeft(nums, target), findRight(nums,target)]
# 3. bisect 包
def searchRange(self, nums: List[int], target: int) -> List[int]:
if not nums:
return [-1, -1]
left,right = bisect.bisect_left(nums, target), bisect.bisect_right(nums, target)
return [left, right - 1] if left < right else [-1, -1]解法的复杂度分析:
Time complexity: O(logN)
Space complexity: O(1)
702. Search in a Sorted Array of Unknown Size
Test cases:
Input: secret = [-1,0,3,5,9,12, ...], target = 9
Output: 4
Explanation: 9 exists in secret and its index is 4.
Input: secret = [-1,0,3,5,9,12, ...], target = 2
Output: -1
Explanation: 2 does not exist in secret so return -1.
这个基本思路跟前面的一样,只有一个判断 end 点在哪,那么我们只需要加一个地方,二分的解法与前面雷同啦!!
def search(self, reader, target):
start, end = 0, 1
# 比target小,就疯狂让end 以次方级别增加
while reader.get(end) < target:
end <<= 1
# 这里用之前的二分解法就可以了,思路不变
...74. Search a 2D Matrix
Test cases:
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false这个题,只需要把二维数组当成一维数组来看,然后就是一个标准的二分查找了。
1. 标准模版
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m = len(matrix)
if m == 0:
return False
n = len(matrix[0])
left, right = 0, m * n - 1
while left <= right:
pivot_idx = (left + right) // 2
# 这里我们根据每一行的长度,来计算出这个pivot_idx在二维数组中的位置
pivot_element = matrix[pivot_idx // n][pivot_idx % n]
if target == pivot_element:
return True
elif target < pivot_element:
right = pivot_idx - 1
else:
left = pivot_idx + 1
return False
# 2. 不死模版
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m = len(matrix)
if m == 0:
return False
n = len(matrix[0])
left, right = 0, m * n - 1
while left + 1 < right:
pivot_idx = (left + right) // 2
# 这里我们根据每一行的长度,来计算出这个pivot_idx在二维数组中的位置
pivot_element = matrix[pivot_idx // n][pivot_idx % n]
if target == pivot_element:
return True
elif target < pivot_element:
right = pivot_idx
else:
left = pivot_idx
if matrix[left // n][left % n] == target:
return True
if matrix[right // n][right % n] == target:
return True
return False
# 3. bisect 包
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
import bisect
if target < matrix[0][0] or target > matrix[-1][-1]:
return False
first_column = [matrix[i][0] for i in range(len(matrix))]
row = bisect.bisect(first_column, target) - 1
if matrix[row][0] == target:
return True
col = bisect.bisect(matrix[row], target) - 1
if matrix[row][col] == target:
return True
return False变种题
153. Find Minimum in Rotated Sorted Array
Test cases:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Input: nums = [1], target = 0
Output: -1思路:这道题也只是一个变种,只需要判断一下,如果 nums[start] < nums[end],那么就是有序的,直接返回 nums[start]就可以了。如果不是有序的,那么就是旋转过的,那么我们就需要判断一下,如果 nums[mid] > nums[mid - 1] and nums[mid] > nums[mid + 1],那么 nums[mid + 1]就是最小值。如果不是,那么我们就需要判断一下,如果 nums[mid] > nums[0],那么说明最小值在右边,否则就在左边。
mid 比最开始的值大
如果 mid 比最开始的值大,那么左边是有序的,最小值在右边
mid 比最开始的值小
如果 mid 比最开始的值小,那么右边是有序的,最小值在左边
# 1. 标准做法
def search(self, nums: List[int], target: int) -> int:
start, end = 0, len(nums) - 1
while start <= end:
mid = start + (end - start) // 2
if nums[mid] == target:
return mid
elif nums[mid] >= nums[start]:
if target >= nums[start] and target < nums[mid]:
end = mid - 1
else:
start = mid + 1
else:
if target <= nums[end] and target > nums[mid]:
start = mid + 1
else:
end = mid - 1
return -1
# 2. 不死循环做法
def findMin(self, nums: List[int]) -> int:
if nums == None and len(nums) == 0:
return -1
start, end = 0, len(nums) - 1
while start + 1 < end:
if nums[start] < nums[end]:
return nums[start]
mid = start + (end - start) // 2
# 因为while条件已经限制了3个元素,所以不用担心mid的边界问题
if nums[mid] > nums[mid - 1] and nums[mid] > nums[mid + 1]:
return nums[mid + 1]
else:
if nums[mid] > nums[0]:
start = mid
else:
end = mid
# 这里需要注意,因为我们是找最小值,所以要比较一下start和end的值
return min(nums[start], nums[end], nums[0])
# 3. bisect 包
import bisect
def search(self, nums: List[int], target: int) -> int:
if len(nums) == 1:
return 0 if nums[0] == target else -1
for i in range(1, len(nums)):
if nums[i-1] > nums[i]:
break
b_po = i
n = -1
if nums[0] <= target <= nums[b_po-1]:
n = bisect.bisect_left(nums[:b_po], target)
else:
n = bisect.bisect_left(nums[b_po:], target)
n = n + b_po
if n != len(nums) and nums[n] == target:
return n
return -1154. Find Minimum in Rotated Sorted Array II
Test case:
Input: nums = [1,3,5]
Output: 1
Input: nums = [2,2,2,0,1]
Output: 0这道题和前面那道题差距并不大,唯一的区别就是,这道题中的数组中可能会有重复的元素,所以我们需要做一下特殊处理,就是如果 nums[mid] == nums[start],那么我们就需要 start += 1,因为这个时候我们并不能确定最小值在哪一边,所以我们就需要 start += 1,然后再进行下一次的循环。
def findMin(self, nums: List[int]) -> int:
if nums == None and len(nums) == 0:
return -1
start, end = 0, len(nums) - 1
while start + 1 < end:
if nums[start] < nums[end]:
return nums[start]
mid = start + (end - start) // 2
if nums[mid] >= nums[mid - 1] and nums[mid] > nums[mid + 1]:
return nums[mid + 1]
else:
if nums[mid] > nums[0]:
start = mid
elif nums[mid] == nums[0]: #
start += 1
else:
end = mid
return min(nums[start], nums[end], nums[0])278. First Bad Version
Test case:
Input: n = 5, bad = 4
Output: 4
Explanation:
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.这道题,仔细看没有什么思路,实际上,就是简单的二分法,只不过这道题的二分法的条件是,如果 mid 是 bad version,那么 end = mid,如果 mid 不是 bad version,那么 start = mid,最后返回 start 或者 end 都可以。
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
start, end = 0, n
while start + 1 < end:
mid = start + (end - start) // 2
if isBadVersion(mid):
end = mid
else:
start = mid
return start if isBadVersion(start) else end答案二分
875. Koko Eating Bananas
Test case:
Input: piles = [3,6,7,11], h = 8
Output: 4
Input: piles = [30,11,23,4,20], h = 5
Output: 30
Input: piles = [30,11,23,4,20], h = 6
Output: 23这道题,其实就是一个二分法的变种,我们需要找到一个最小的速度,使得 Koko 能够在 h 小时内吃完所有的香蕉,那么我们就可以使用二分法,来找到这个最小的速度。
def minEatingSpeed(self, piles: List[int], h: int) -> int:
def isValidSpeed(piles, speed, h):
total = 0
for item in piles:
total += (item + speed - 1) // speed
if total > h:
return False
return True
if len(piles) > h:
return -1
start, end = 1, 1000000000
while start + 1 < end:
mid = start + (end - start) // 2
if isValidSpeed(piles, mid, h):
end = mid
else:
start = mid
if isValidSpeed(piles, start, h):
return start
if isValidSpeed(piles, end, h):
return end
return -1
1283. Find the Smallest Divisor Given a Threshold
Test case:
Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4 we can get a sum to 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).这道题,其实就是一个二分法的变种,我们需要找到一个最小的 divisor,使得 sum((item + divisor - 1) // divisor for item in nums) <= threshold,那么我们就可以使用二分法,来找到这个最小的 divisor。
def smallestDivisor(self, nums: List[int], threshold: int) -> int:
start, end = 1, 1000000
while start + 1 < end:
output = 0
mid = start + (end - start) // 2
if sum((item + mid - 1) // mid for item in nums) <= threshold:
end = mid
else:
start = mid
if sum((item + start - 1) // start for item in nums) <= threshold:
return start
if sum((item + end - 1) // end for item in nums) <= threshold:
return end
return start







Comments NOTHING