前言

这个专题只用来总结binary tree的recursive 做法。

recursive的做法，看似代码简洁，实则要考虑的方面有很多。通常设计一个recusive的做法，需要考虑到以下三个步骤：

1. 递归的终止条件 (base condition)：要考虑什么时候停止递归
2. 递归的递推公式 (recursion formula)：要考虑递推的是什么，怎么进入下一层递归
3. 递归的返回值 (return value)：要考虑返回的是什么，是什么类型，是什么值

基础题目

↓点击题目就可以直接跳转到leetcode题目页面↓

104. Maximum Depth of Binary Tree

test cases:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Input: root = [1,null,2]
Output: 2

我们先想一个不那么精致的解法，考虑到所有的情况：

def maxDepth(self, root: Optional[TreeNode]) -> int:
    if not root: # base condition
        return 0

    if not root.left and not root.right: # base condition
        return 1

    if not root.left: # recursion formula
        return 1 + self.maxDepth(root.right)

    if not root.right: # recursion formula
        return 1 + self.maxDepth(root.left)

    # recursion formula and return value
    return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

为什么说这个解法不够精致呢，因为他有可以合并的地方，比如中间这三个条件，可以合并成一个条件。原因就是因为这三个条件的base condition都是一样的，所以可以合并成一个条件：

if not root.left and not root.right: # base condition
    return 1

if not root.left: # recursion formula
    return 1 + self.maxDepth(root.right)

if not root.right: # recursion formula
    return 1 + self.maxDepth(root.left)

这样就可以得到一个更精致的解法：

def maxDepth(self, root: Optional[TreeNode]) -> int:
    if root == None: return 0

    leftMax = self.maxDepth(root.left)
    rightMax = self.maxDepth(root.right)

    return max(leftMax, rightMax) + 1

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数
• 空间复杂度：O(N), 最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）

111. Minimum Depth of Binary Tree

test cases:

Input: root = [3,9,20,null,null,15,7]
Output: 2

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

这道题和前面的题目不同的是，这道题需要考虑更多的情况，假如一个节点只有一个左子树或者右子树，那么要使用max来计算深度，而不是min。所以这道题的递归公式要考虑的情况更多：

def minDepth(self, root):
    if not root:
        return 0
    if None in [root.left, root.right]:
        return max(self.minDepth(root.left), self.minDepth(root.right)) + 1
    else:
        return min(self.minDepth(root.left), self.minDepth(root.right)) + 1

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

100. Same Tree

test cases:

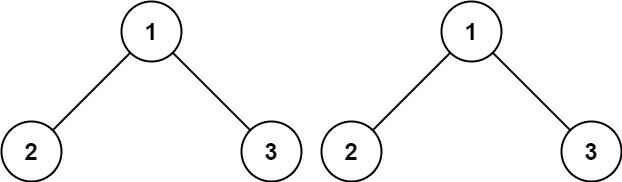
Input: p = [1,2,3], q = [1,2,3]
Output: true

Input: p = [1,2], q = [1,null,2]
Output: false

同样，这道题需要考虑的情况也比较多，因为要判断两个树是否相同，需要考虑的情况就有：

1. 两个树都是空树
2. 有一个树是空树
3. 两个树都不是空树，但是根节点的值不同
4. 两个树都不是空树，根节点的值相同

所以这道题的递归公式要考虑的情况得出的代码就是

def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
    if not p and not q: # base condition 1
        return True

    if not p or not q: # base condition 2
        return False

    if p.val != q.val: # base condition 3
        return False

    # recursion formula
    return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

101. Symmetric Tree

test cases:

Input: root = [1,2,2,3,4,4,3]
Output: true

Input: root = [1,2,2,null,3,null,3]
Output: false

这道题和上一道题的思路是一样的，也是需要考虑的情况比较多，不过要注意的是，这道题的递归公式是不一样的，因为这道题是判断两个树是否对称，所以需要使用一个子函数来递归判断对称条件：

1. 两个树都是空树
2. 有一个树是空树
3. 两个树都不是空树，但是根节点的值不同
4. 左边的树的左子树和右边的树的右子树不对称

所以这道题的递归公式要考虑的情况得出的代码就是

def isSymmetric(self, root: Optional[TreeNode]) -> bool:
    def _is_sym(left, right):
        if not left and not right:
            return True
        if not left and right:
            return False
        if not right and left:
            return False
        if left.val != right.val:
            return False
        left_res = _is_sym(left.left, right.right)
        right_res = _is_sym(left.right, right.left)
        return left_res and right_res

    if not root:
        return True

    return _is_sym(root.left, root.right)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

226. Invert Binary Tree

test cases:

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Input: root = [2,1,3]
Output: [2,3,1]

这道题只需要在原先的树上进行修改，不过要注意的是，这里的替换需要使用一个临时变量来存储，不然会出现错误。或者使用python的特性，直接交换两个变量的值：

def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
    if not root:
        return

    root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
    return root

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

110. Balanced Binary Tree

Input: root = [3,9,20,null,null,15,7]
Output: true

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Input: root = []
Output: true

这道题的思路是，如果当前节点是叶子节点，那么返回当前节点的值，如果不是叶子节点，那么返回左子树或者右子树的和加上当前节点的值。

def isBalanced(self, root: Optional[TreeNode]) -> bool:
    if not root:
        return True

    def dfs(root):
        if not root:
            return 0

        left = dfs(root.left)
        right = dfs(root.right)

        if left == -1 or right == -1 or abs(left - right) > 1:
            return -1

        return max(left, right) + 1

    return dfs(root) != -1

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

高级类型题

114. Flatten Binary Tree to Linked List

test cases:

Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Input: root = []
Output: []

这道题的思路是，先把左子树flatten，然后把右子树flatten，然后把左子树放到右子树的位置，然后把原来的右子树放到左子树的最右边的节点的右子树的位置。

def flatten(self, root: Optional[TreeNode]) -> None:
    """
    Do not return anything, modify root in-place instead.
    """
    if not root:
        return None

    self.flatten(root.left)
    self.flatten(root.right)

    left = root.left
    right = root.right

    root.left = None
    root.right = left

    p = root
    while p.right:
        p = p.right
    p.right = right

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

116. Populating Next Right Pointers in Each Node

test cases:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]

Input: root = []
Output: []

这道题的思路是，先把左子树的next指针指向右子树，然后把右子树的next指针指向父节点的next的左子树，然后递归的处理左子树和右子树。

def connect(self, root: 'Node') -> 'Node':
    if not root:
        return None

    if root.left:
        root.left.next = root.right
        if root.next:
            root.right.next = root.next.left

    self.connect(root.left)
    self.connect(root.right)

    return root

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

117. Populating Next Right Pointers in Each Node II

test cases:

Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]

Input: root = []
Output: []

这道题和上面的题的思路是一样的，只不过这道题的树不是完全二叉树，所以需要判断一下左子树和右子树是否存在。

def connect(self, root: 'Node') -> 'Node':
    if not root:
        return None

    if root.left:
        if root.right:
            root.left.next = root.right
        else:
            p = root.next
            while p:
                if p.left:
                    root.left.next = p.left
                    break
                elif p.right:
                    root.left.next = p.right
                    break
                p = p.next

    if root.right:
        p = root.next
        while p:
            if p.left:
                root.right.next = p.left
                break
            elif p.right:
                root.right.next = p.right
                break
            p = p.next

    self.connect(root.right)
    self.connect(root.left)

    return root

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

297. Serialize and Deserialize Binary Tree

test cases:

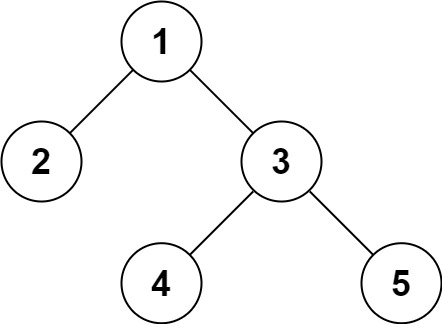
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Input: root = []
Output: []

这道题的思路是，先序遍历树，然后把遍历的结果保存到一个数组中，然后再把这个数组转换成字符串，然后再把这个字符串转换成数组，然后再把这个数组转换成树。

def serialize(self, root: Optional[TreeNode]) -> str:
    if not root:
        return ""

    res = []
    def preorder(root):
        if not root:
            res.append("null")
            return

        res.append(str(root.val))
        preorder(root.left)
        preorder(root.right)

    preorder(root)
    return ",".join(res)

def deserialize(self, data: str) -> Optional[TreeNode]:
    if not data:
        return None

    data = data.split(",")
    def buildTree(data):
        if not data:
            return None

        val = data.pop(0)
        if val == "null":
            return None

        root = TreeNode(int(val))
        root.left = buildTree(data)
        root.right = buildTree(data)

        return root

    return buildTree(data)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

110. Balanced Binary Tree

test cases:

Input: root = [3,9,20,null,null,15,7]
Output: true

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

这道题的思路是，先序遍历树，然后把遍历的结果保存到一个数组中，然后再把这个数组转换成字符串，然后再把这个字符串转换成数组，然后再把这个数组转换成树。

def isBalanced(self, root: Optional[TreeNode]) -> bool:
    def height(root):
        if not root:
            return 0

        return max(height(root.left), height(root.right)) + 1

    if not root:
        return True

    return abs(height(root.left) - height(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

复杂度分析：

• 时间复杂度：O(N^2)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

236. Lowest Common Ancestor of a Binary Tree

test cases:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

这道题的思路是，先序遍历树，然后把遍历的结果保存到一个数组中，然后再把这个数组转换成字符串，然后再把这个字符串转换成数组，然后再把这个数组转换成树。

def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
    if not root or root == p or root == q:
        return root

    left = self.lowestCommonAncestor(root.left, p, q)
    right = self.lowestCommonAncestor(root.right, p, q)

    if left and right:
        return root

    return left if left else right

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

前序遍历，中序遍历，后序遍历类型题

首先我们来复习一下前序遍历，中序遍历，后序遍历的定义：

• 前序遍历：根节点 -> 左子树 -> 右子树
• 中序遍历：左子树 -> 根节点 -> 右子树
• 后序遍历：左子树 -> 右子树 -> 根节点

举一个例子来说就是：

    1
   / \
  2   3
 / \ / \
4  5 6  7

• 前序遍历：1 2 4 5 3 6 7
• 中序遍历：4 2 5 1 6 3 7
• 后序遍历：4 5 2 6 7 3 1

那么我们来看一下这道题：

105. Construct Binary Tree from Preorder and Inorder Traversal

test cases:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Input: preorder = [-1], inorder = [-1]
Output: [-1]

这道题的重点，就是关注preorder 前序遍历的第一个元素，就是根节点，然后在inorder 中找到这个根节点，然后就可以确定左子树和右子树的范围了，然后就可以递归的构建树了。

def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
    if not preorder or not inorder:
        return None

    index = inorder.index(preorder.pop(0))
    root = TreeNode(inorder[index])
    root.left = self.buildTree(preorder, inorder[:index])
    root.right = self.buildTree(preorder, inorder[index+1:])

    return root

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

106. Construct Binary Tree from Inorder and Postorder Traversal

test cases:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Input: inorder = [-1], postorder = [-1]
Output: [-1]

这道题和上一道题的思路是一样的，只不过这道题的根节点是postorder的最后一个元素，然后在inorder中找到这个根节点，然后就可以确定左子树和右子树的范围了，然后就可以递归的构建树了。

# 1. 普通做法
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not inorder or not postorder:
            return None

        index = inorder.index(postorder.pop())
        root = TreeNode(inorder[index])
        root.right = self.buildTree(inorder[index+1:], postorder)
        root.left = self.buildTree(inorder[:index], postorder)

        return root

# 2. 做法二： 优化空间复杂度
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
    map_inorder = {}
    for i, val in enumerate(inorder): map_inorder[val] = i
    def recur(low, high):
        if low > high: return None
        x = TreeNode(postorder.pop())
        mid = map_inorder[x.val]
        x.right = recur(mid+1, high)
        x.left = recur(low, mid-1)
        return x
    return recur(0, len(inorder)-1)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

889. Construct Binary Tree from Preorder and Postorder Traversal

test cases:

Input: pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
Output: [1,2,3,4,5,6,7]

这道题和上面两道题的思路是一样的，只不过这道题的根节点是preorder的第一个元素，然后在postorder中找到这个根节点，然后就可以确定左子树和右子树的范围了，然后就可以递归的构建树了。

def constructFromPrePost(self, pre: List[int], post: List[int]) -> Optional[TreeNode]:
    if not pre or not post:
        return None

    root = TreeNode(pre.pop(0))
    if len(pre) == 0:
        return root

    index = post.index(pre[0])
    root.left = self.constructFromPrePost(pre[:index+1], post[:index+1])
    root.right = self.constructFromPrePost(pre[index+1:], post[index+1:-1])

    return root

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同

Sum 类型题

112. Path Sum

test cases:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true

Input: root = [1,2,3], targetSum = 5
Output: false

Input: root = [1,2], targetSum = 0
Output: false

这道题的思路是，如果当前节点是叶子节点，那么判断当前节点的值是否等于targetSum，如果不是叶子节点，那么判断左子树或者右子树是否存在路径和等于targetSum减去当前节点的值。

def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
    if not root:
        return False

    if not root.left and not root.right:
        return root.val == targetSum

    return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

113. Path Sum II

test cases:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]

Input: root = [1,2,3], targetSum = 5
Output: []

Input: root = [1,2], targetSum = 0
Output: []

这道题的思路是，如果当前节点是叶子节点，那么判断当前节点的值是否等于targetSum，如果不是叶子节点，那么判断左子树或者右子树是否存在路径和等于targetSum减去当前节点的值，如果存在，那么把当前节点的值加入到路径中。

def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
    if not root:
        return []

    res = []
    def dfs(root, targetSum, path):
        if not root:
            return

        if not root.left and not root.right:
            if root.val == targetSum:
                res.append(path + [root.val])
            return

        dfs(root.left, targetSum - root.val, path + [root.val])
        dfs(root.right, targetSum - root.val, path + [root.val])

    dfs(root, targetSum, [])
    return res

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

437. Path Sum III

test cases:

Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3

这道题的思路是，如果当前节点是叶子节点，那么判断当前节点的值是否等于targetSum，如果不是叶子节点，那么判断左子树或者右子树是否存在路径和等于targetSum减去当前节点的值，如果存在，那么把当前节点的值加入到路径中。

def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
    if not root:
        return 0

    def dfs(root, targetSum):
        if not root:
            return 0

        res = 0
        if root.val == targetSum:
            res += 1

        res += dfs(root.left, targetSum - root.val)
        res += dfs(root.right, targetSum - root.val)

        return res

    return dfs(root, targetSum) + self.pathSum(root.left, targetSum) + self.pathSum(root.right, targetSum)

复杂度分析：

• 时间复杂度：O(N^2)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度），每次调用都需要遍历整棵树
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

666. Path Sum IV

未完待续

129. Sum Root to Leaf Numbers

test cases:

Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

这道题的思路是，如果当前节点是叶子节点，那么返回当前节点的值，如果不是叶子节点，那么返回左子树或者右子树的和加上当前节点的值。

def sumNumbers(self, root: Optional[TreeNode]) -> int:
    if not root:
        return 0

    def dfs(root, path):
        if not root:
            return 0

        if not root.left and not root.right:
            return path * 10 + root.val

        return dfs(root.left, path * 10 + root.val) + dfs(root.right, path * 10 + root.val)

    return dfs(root, 0)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

124. Binary Tree Maximum Path Sum

test cases:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

这道题的思路是，如果当前节点是叶子节点，那么返回当前节点的值，如果不是叶子节点，那么返回左子树或者右子树的和加上当前节点的值。

def maxPathSum(self, root: Optional[TreeNode]) -> int:
    if not root:
        return 0

    self.res = float('-inf')

    def dfs(root):
        if not root:
            return 0

        left = max(0, dfs(root.left))
        right = max(0, dfs(root.right))

        self.res = max(self.res, left + right + root.val)

        return max(left, right) + root.val

    dfs(root)
    return self.res

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间

222. Count Complete Tree Nodes

test cases:

Input: root = [1,2,3,4,5,6]
Output: 6

Input: root = []
Output: 0

Input: root = [1]
Output: 1

这道题的思路是，如果当前节点是叶子节点，那么返回当前节点的值，如果不是叶子节点，那么返回左子树或者右子树的和加上当前节点的值。

def countNodes(self, root: Optional[TreeNode]) -> int:
    if not root:
        return 0

    def dfs(root):
        if not root:
            return 0

        left = dfs(root.left)
        right = dfs(root.right)

        return left + right + 1

    return dfs(root)

复杂度分析：

• 时间复杂度：O(N)，N是树的节点数，考虑到最坏情况下，树是完全不平衡的，递归会调用N次（树的高度）
• 空间复杂度：O(N), 与时间复杂度相同，原因是递归调用栈的空间